In the year 1821, German Physicist namely ‘Thomas Seebeck noticed various thermoelectric effect properties. He noticed that an electrical circuit with two dissimilar metals with different temperatures created an EMF at their junctions. Thomas Seebeck observed that the compass needle deflected when he created a closed loop between two different metals, forming a thermocouple. The circuit generates a current known as the thermoelectric current. Previously, people believed that the compass needle deflected due to the induced magnetic field caused by temperature variation, a phenomenon called the thermo-magnetic effect. After that, Hans Christian Orsted recognized that deflection was because of the induced current. The thermoelectric effect contains three main effects: Seebeck, Peltier & Thomson effects. This article discusses an overview of the Seebeck Effect, derivation, and its applications.
What is the Seebeck Effect?
The Seebeck effect can be defined as the process where the temperature variation between two different electrical conductors or semiconductors produces a voltage variation between the two substances. This effect explains the electromotive force generation & the electric current within a loop featuring a minimum of two different conductors at two different temperatures, called thermocouples. Thus, it can be called the Seebeck effect thermocouple.
Whenever heat is provided to one of the two semiconductors or conductors, then heated electrons can flow in the direction of the cooler one. If the pair of semiconductors is connected through an electrical circuit, then direct current is supplied throughout that circuit. So the voltages generated by the Seebeck effect are very small, generally a few microvolts only per kelvin of temperature variation at the junction. If the temperature variation is huge enough, then some Seebeck-effect devices generate a few millivolts.
This effect can also be reversed. For instance, whenever the hot & cold circuit junctions are exchanged, then the current flow direction can also change. Thus, the thermoelectric effect can be a reversible process. The magnitude & thermocouple EMF sign mainly depend on the metals utilized & the temperature of the cold & hot junctions.
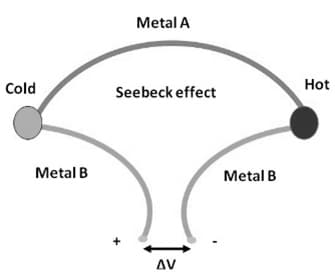
Seebeck Effect
Seebeck Effect Formula
You can derive this formula from the Seebeck coefficient, a material property that quantifies the magnitude of the effect. Therefore, you can represent the Seebeck effect formula as:
V = S × ΔT
Where:
‘V’ is the voltage generated in volts.
‘S’ is the coefficient of Seebeck in volts per Kelvin.
‘ΔT’ is the difference in temperature between the two conductor ends.
The Seebeck coefficient changes with the temperature & the material type utilized. Generally, metals have a minor Seebeck coefficient as compared to semiconductors. As a result, the Seebeck coefficient sign specifies the polarity of the voltage generated. So when the temperature rises then the voltage will be positive. The Seebeck efficiency is 5 to 8%.
Explanation of the Seebeck Effect
We know that the Seebeck effect is a phenomenon where a temperature variation between two dissimilar conductors can result in electric voltage generation. This effect is also called the thermoelectric effect.
This effect can be caused by the heat flow from a hot area to a cooler area within a material. Whenever a temperature variation exists across a material, then electrons within the material can turn more active in the hot region & less active in the cold region. This causes electrons to flow from the hot region to the cold region, which creates a voltage variation between the two regions.
The Seebeck effect works on the thermoelectricity principle, which is the main relationship between electrical potential & temperature. Whenever two dissimilar conductors with dissimilar temperatures come into contact, and then electrons within the hot conductor will get energy & shift toward the cooler conductor. Thus, this creates a voltage difference between the two conductors & current supplies throughout the electric circuit.
The generated voltage’s magnitude by the Seebeck effect is simply proportional to the temperature variation between the two conductors & the conductors’ properties themselves. The Seebeck coefficient explains the main relationship between voltage and temperature variation. You can define the Seebeck coefficient as the ratio of the voltage generated to the temperature difference between the two conductors..
Difference b/w Seebeck Effect and Peltier Effect
The difference between the Seebeck effect and the Peltier effect includes the following.
Seebeck Effect | Peltier Effect |
| Seebeck effect describes a temperature variation between two dissimilar electrical semiconductors or conductors that generates a voltage variation between the two substances | The Peltier effect occurs upon the formation of a temperature variation between the junctions by applying a voltage variation between the terminals. |
| Thomas Johann Seebeck, a Baltic German physicist, gave his name to this effect. | Jean Charles Athanase Peltier, a French physicist, also contributed to the naming of another related effect. |
| This effect occurs mainly whenever the two thermocouple ends are at dissimilar temperatures, and it results flow of electricity from the hot to the cold metal. | The Peltier effect occurs when an electrical current supplies across the two terminals, forming a temperature variation between the junctions. |
| This Effect helps us in calculating the generated electromotive field by a device. | The Peltier effect helps in achieving thermoelectric cooling. |
| The Seebeck principle is the Thermoelectric effect because of a temperature gradient. | The Peltier Effect principle is the thermoelectric effect because of an electric current |
| It can cause Temperature variation along a conductor. | It can cause an Electric current to flow throughout a junction of two different conductors. |
| This effect is useful in measuring temperature with large sensitivity & accuracy to produce electric power mainly for special applications. | Several thermal cyclers and laboratory devices use the Peltier effect to amplify DNA through the PCR (Polymerase Chain Reaction). |
| It generates voltage. | This effect generates or absorbs heat. |
| Its directionality is unidirectional and depends mainly on the temperature gradient. | Its directionality is bidirectional and depends mainly on the current direction. |
| The voltage generated in this effect is proportional to temperature variation. | The heat released or absorbed in this effect is proportional to the current. |
| Efficiency in this effect is related to the conversion of heat to electricity, | Efficiency in the Peltier effect is related to the alteration of electricity to heat. |
| The applications of this effect are: Thermocouples, thermoelectric power generation & thermopiles. | Peltier effect applications are: heating or Cooling devices, thermoelectric coolers, etc. |
Seebeck Coefficients
The Seebeck coefficient is a measurement of the magnitude of an induced thermoelectric voltage in reply to a temperature variation across that material, induced through the Seebeck effect. The SI unit of this coefficient is volts/kelvin; however, it is more frequently given within microvolts/kelvin. The Seebeck coefficient mainly depends upon the metal’s work function within the circuit, scattering mechanism, and electron densities on the metal.
Mathematically Seebeck coefficient can be stated as;
ΔV = SAB(Th−Tc)
Where,
‘Th’ is the Warmer end temperature.
‘Tc’ is the Cooler end temperature.
ΔV is the developed potential across the two ends.
SAB is the Seebeck coefficient.
When the conductor maintains its two points at various temperatures, charge carriers in the hotter region move to the colder region and diffuse. So, any electric field created will stop this diffusion because the migration of charge carriers has created a strong field. Below are the Seebeck coefficients for different metals at zero degrees Celsius.
Material | Seebeck Coefficient |
Sodium | -2 |
Bismuth | -72 |
Potassium | -9 |
Nickel | -15 |
| Carbon | 3 |
| Lead | 4 |
| Silver | 6.5 |
Mercury | 0.6 |
Aluminium | 3.5 |
| Selenium | 900 |
| Antimony | 47 |
Copper | 6.5 |
Gold | 6.5 |
Silicon | 440 |
| Tellurium | 500 |
| Germanium | 300 |
Seebeck Effect Example
Let us consider a practical example of this effect to demonstrate the generated voltage calculation with the Seebeck effect formula. People use a thermocouple made with two different metals – iron and copper – where they connect these metals at their two ends to form a temperature gradient among the two junctions.
If we consider the Seebeck coefficient of Cu (copper) is 1.8 μV/K & the Seebeck coefficient of Fe (iron) is 20 μV/K. So the temperature at the hot junction is 500 K whereas the temperature at the cold junction is 400 K.
Here, the overall Seebeck coefficient is determined by subtracting the copper Seebeck coefficient from the iron:
Stotal = SFe – SCu
Substituting the values given in the above formula, we can get
Stotal = 20 μV/K – 1.8 μV/K = 18. 2 μV/K
Now by the Seebeck effect formula, we can measure the generated voltage; V = S × ΔT
Where ‘ΔT’ is the temperature difference between the cold & hot junctions:
ΔT = Thot – Tcold = 500 K – 400 K = 100 K
By substituting these values in the above formula, we can get;
V = 18. 2 μV/K × 100 K = 1820 μV
Therefore, the voltage generated across the thermocouple is 1820 μV (or 1. 82 mV).
The above example shows how the Seebeck effect formula measures the generated voltage with a thermocouple. Furthermore, users can use the formula in different applications such as generating thermoelectric power and sensing temperature.
Advantages & Disadvantages
The advantages of the Seebeck effect include the following.
- This is versatile, reliable & simple.
- It does not need any external power sources or moving parts.
- This effect operates above a wide range of materials & temperatures.
- It generates electricity using low-grade heat sources.
The disadvantages of the Seebeck effect include the following.
- This is incomplete because of the accessibility & compatibility of materials.
- This effect needs high electrical conductivity materials.
- It also needs materials including different Seebeck coefficients to make a voltage difference.
- The Seebeck coefficient is one of the properties that mainly depends on the type & attention of charge carriers, their connections through the lattice & their energy levels.
- The Seebeck coefficient changes with composition, magnetic field & temperature.
- Its efficiency is quite low at <10%, so a small input heat portion is changed into electricity.
- The materials utilized in thermoelectric devices can be costly, particularly for high-temperature-based applications.
It has a low power density.
Applications
The applications of the Seebeck effect include the following.
- The Seebeck effect is applicable in thermocouples, temperature sensors & thermoelectric generators.
- In thermoelectric generators, power plants and industries use this effect to prevent the remaining heat from being wasted.
- In thermocouples, this effect calculates temperature differences and controls electronic switches that power the system.
- Automobile industries utilize this effect to improve fuel efficiency.
- This effect measures potential variations between two semiconductors. The thermocouple Seebeck effect is frequently used.
What is the Seebeck effect used for?
The Seebeck effect powers thermocouples to measure temperature differences and to control electronic switches that manage the system’s power.
What is the Seebeck coefficient formula?
The Seebeck coefficient (S) defines the coefficient in the relationship between the temperature gradient (∇T) and the electrical field (E) in a conducting material, where the net current is zero throughout the sample.
Why does the Seebeck effect occur?
The Seebeck effect occurs mainly by the thermal gradient between two materials & the variation within their electrical conductivities.
Why does Seebeck increase with temperature?
The Seebeck coefficient value is positive over the range of measured temperature, which demonstrates p-type performance, and it increases with the temperature. When the temperature increases, electrical conductivity can also increase indicating semiconductor behavior.
Why is the Seebeck effect used in thermocouple operation?
A temperature variation between the ends of a thermocouple causes electricity to be formed, known as the Seebeck effect.
Thus, this is an overview of the Seebeck effect, formula, explanation, differences, advantages, disadvantages, and its applications. This effect occurs when two dissimilar conductors or semiconductors are coupled in a loop and there is a temperature difference between their junctions, they generate an electric potential. The electric potential is proportional to the difference in temperature & depends mainly on the used materials. This effect is the basis for thermoelectric generators, pin caloritronics & thermocouples. Here is a question for you, what is the Peltier effect?