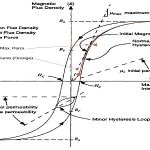
The term 'Hysteresis' was derived from the Ancient Greek Word and the meaning of this term is a deficiency of leg behind. While defining the property of magnetic material, “James Alfred Ewing” proposed this term in the year 1890. The property of hysteresis is observed in the concepts of chemistry, economics, physics, and engineering as well. This characteristic was included in most of the artificial systems such as in Schmitt triggers and … [Read more...]
What is a Displacement Current : Formula & Its Significance
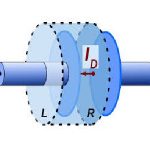
In the field of electromagnetism, let us assume that the electric displacement field is given by D. The electric field can be observed across a conductor, or in a vacuum space. Vacuum in the sense if they assume that we have connected a capacitor, then the gap between the plates is assumed as a vacuum. After some time, once the capacitor is charged, even if we remove the source, there exists some amount of electric field across the plates of the capacitor. … [Read more...]