Electric flux is a basic concept within physics that assists us in understanding as well as measuring the electric field supplied throughout a given surface. This is an electric field property in the number of electric force lines intersecting a given region. This flux gives a means to explain electric field lines flow throughout an area. Electric field lines are simply considered to originate on positive electric charges & to terminate on negative charges. The field lines are directed simply into a closed surface which is considered as negative; the field lines are directed out of a closed surface is considered as positive. This article provides brief information on electric flux.
What is Electric Flux?
The measure of electric field lines supplying throughout a specified closed surface is known as electric flux (Φ). It is a scalar quantity that represents the whole number of electric field lines supplied throughout a given surface. This is denoted by the Greek letter ‘Φ’ (phi).
The estimation of the whole number of electric field lines is the electric flux that passes throughout a specified closed surface. It is a vector quantity including a direction. The ‘Φ’ is considered to have a sign linked with it which indicates whether the electric field lines are going into the surface (or) coming out from the surface.
Electric Flux
Formula
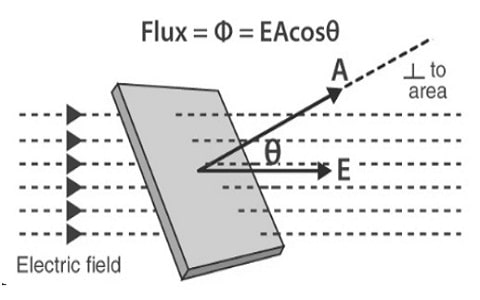
The concept of electric flux mainly depends on various parameters like; the power of the electric force lines, the surface area & also on the direction between the surface region and the electric force lines. So all these quantities jointly yield electric fields throughout the surface & the equation of ‘Φ’ is;
Φ = E • A (or) Φ = E A cos θ
Where,
‘Φ’ is the electric flux,
‘E’ is the strength of the electric field.
‘A’ is the closed surface area.
‘θ’ is the angle between the electric field lines & the area vector.
Some factors that affect electric flux are discussed below.
Electric Field Strength: It is denoted with ‘E’and Φ ∝ Electric Field Strength E, therefore it increases with the increase within electric field lines.
Surface Area: It is denoted with ‘A” and Φ ∝ surface area A, so its magnitude is enhanced when the area increases.
Cos θ: It achieves the highest value of ‘1’ for θ = 0 & smallest value of ‘-1’ for θ = 180.
Types of Electric Flux
It is available in two types based on the angle between the field lines & the area vector like positive electric flux and negative electric flux which are discussed below.
Positive Electric Flux
Whenever the electric field lines pass outer through a closed surface, then ‘Φ’ can be considered as positive electric flux. This flux mainly occurs whenever the electric field lines are within a similar way as the normal vector outward-pointing to the surface.
Negative Electric Flux
Whenever the electric field lines pass inward throughout a closed surface, then it is considered as negative ‘Φ’. So this happens mainly whenever the electric field lines are within the reverse direction to the normal vector outward-pointing to the surface.
Properties
The properties of electric flux lines help in understanding & analyzing electric fields which are discussed below.
- It has magnitude only without direction. So it quantifies the whole number of electric field lines supplying throughout a specified surface, regardless of its way.
- The ‘Φ’ throughout a surface is directly proportional to the power of the electric field supplied throughout the ‘E’ surface. A stronger electric field results in high electric flux throughout the surface.
- It depends on the point of view between the area vector as well as the field lines.
- It simply follows the superposition principle that the whole flux throughout a surface is the sum of the individual fluxes throughout various surface parts.
Electric Flux with Different Surfaces
The main relation between Φ (flux), E (Field Strength) & net area within the field direction (A cosθ) as Φ = E A cos θ. Thus it is very clear that electric flux throughout the surfaces mainly depends on the surface area. In addition, according to the ‘Gauss law’, the whole flux passing throughout a closed surface mainly depends on the net-surrounded charge,
Φ = qenclosed / ε0
Where ‘qenclosed’ is the whole charge enclosed within the surface. Now, are going to discuss the ‘Φ’ throughout the open & closed surface are discussed below.
Flux with Closed Surfaces
A closed surface can be defined as; any surface that encloses totally a three-dimensional region. The main examples of this surface are; spheres, cylinders, cubes, etc. According to Gauss’s Law, understanding these surfaces is very critical in understanding the main relationship between the whole electric flux supplying throughout a surface & the charge enclosed in it.
The whole electric flux according to Gauss’s Law through a closed surface can be proportional to the whole charge enclosed through that surface, separated by the medium permittivity. The closed surfaces’ symmetric nature simplifies the measurement of electric flux by enabling straightforward Gauss’s Law application.
Φ = qenclosed/ε
Where,
‘q’ is the whole charge enclosed in a closed surface and ‘ε’ is the medium permittivity.
Flux with Open Surfaces
These surfaces have open boundaries so it doesn’t contain a volume. The direct Gauss’s Law application will turn difficult in open surfaces case, and hence determining the flux throughout open surface needs mixing of the electric field’s dot product & the surface area vector above the whole surface.
These calculations are very difficult as compared to the closed surfaces because of the lack of symmetry. They involve integrating more than irregularly shaped surfaces. These surfaces mainly include; sheets, planes, rings, and many more.
The flux ‘Φ’ throughout an open surface is simply determined with the following integral calculation:
Φ = ∲ E.dA
Where,
‘E’ is the electric field.
‘dA’ is the small region element from the surface.
The electric field & the differential area vector dot product are integrated above the open surface to analyze the total flux.
Applications
The applications of electric flux include the following.
- Electric flux in Gauss’s law plays a major role because, it relates to the entire ‘Φ’ throughout a closed surface and the whole charge enclosed within the surface.
- This flux is used to understand the capacitor’s behavior which stores energy.
- It is used in the electromagnetic induction study. Whenever a magnetic field flowing throughout a closed loop changes, it induces an electric field, and the flux concept helps understand the induced electromotive force.
- This flux plays an essential role in studying dielectric materials.
What is meant by electric flux?
The property of an electric field is Electric flux, defined as the number of electric field lines that intersect a specified region. Electric field lines start with positive charges & end with negative charges.
Is electric flux equal to charge?
The ‘Φ’ is a measure of the quantity flow throughout a given region, whereas charge is a basic property of material. Flux can be positive (or) negative but charge can be only positive (or) negative based on the kind of charge.
Is electric flux a vector?
It is not a vector quantity but it is a scalar quantity.
Is Weber SI unit of electric flux?
No, the SI unit of ‘Φ’ is volt-metres but Weber is the SI unit of magnetic flux.
How do you find flux?
The flux can be found through a surface by using different formulas like ∫∫SF⋅(Tu×Tv)dA and using strokes theorem like; ∫∫S(∇×F)⋅dS.
Thus, this is an overview of electric flux, working, and its applications. The concept of ‘Φ is used with Gauss’ law where the term ‘flux’ is derived simply from the Fluxus Latin word that means flow. It is measured simply in coulombs like the electric charge. Electric flux is electric field line measurement through a specified surface. The whole ‘Φ’ from a closed surface equals the enclosed charge separated by the permittivity. The electric flux SI unit is voltmeters & its formula is ΦE => E.A = EAcosθ. Here is a question for you, what is Gauss Law?