The basic relationship between an electric current as well as a magnetic field is stated by the scientist’s biot & savart. This is the basic of magnetostatics that plays the main role that is the same as to coulomb’s law. The inventors of this law conducted various experiments by using the needle of compass deflection to measure the strength of the magnetic field of an electric current, changing in both shape & magnitude and came to the conclusion that an element which carries current will project a magnetic field into space. The equation of Biot savart law gives a magnetic field by a current-carrying coil which calculates its strength at different points on space.
What is Biot Savart Law?
Biot Savart Law definition is that it is the relationship between an electric current and magnetic field by which magnetic flux density at a point can be determined.
Derivation or Formula of Biot Savart Law
The expression for flux density or magnetic flux induction was derived by Biot and savart and is given as
dB = (I.dl. sinα) /r2
Explanation of Biot Savart Law
Consider a conductor in which current ‘I’ is flowing which produces a magnetic field. In order to move the charge, a certain length of the path should be defined.
The length of the path is defined by ‘dl’. The flow of current through the conductor at ‘dl’ produces a magnetic field around it.
The current element is represented by ‘I.dl’ all the current elements put together to make a conductor. The current element is the preliminary thing that is necessary to create a magnetic field.
Consider a point ‘A’ in space which is at a distance ‘r’ with respect to the current element. ‘α ‘ is the angle between the vector ‘dl’ and ‘r’ as shown in the figure.
The strength of the magnetic field at point ‘A’ is determined by ‘dB’. To find the magnetic field at point ‘A’ Biot and savart derived a law I,e Biot savart law.
Relation Between Magnetic Field and Current Element
The magnetic field is directly proportional to the current flowing and also proportional to the length of the current element.
dB α I. dl
The more the amount of current passage, the more will be the magnetic field.
Relation Between Magnetic Field and Radius
The magnetic field is inversely proportional to the distance between the Point ‘A’ and the current element ‘dl’.
More the distance between them less will be a magnetic field and vice-versa.
dB α 1/r2
Relation Between Magnetic Field and Angle Between ‘dl’ and ‘r’
The magnetic field at all ‘r’ distances is not the same it might become strong or weak depending upon the value of angle ‘α’. The magnetic field is maximum when the value of angle ‘α’ is 90°and it is minimum if the value of angle ‘α’ is 0°.
dB α sinα
All these collectively put together as
Db = K.I. dl.sinα /r2
Where,
I = current of element
dL = Change in length
α = angle between the current element and distance between the point ‘A’.
The property of space which allows a certain amount of magnetic field at a point, such characteristic of space is known as permeability which is represented by ‘µ’.
Db = K I dl sinα/ r2
Where K = proportionality constant
K = µ 0 µ r /4π
Where µ 0 = permeability of free space,
µ r = relative permeability,
Db = (µ 0. µ r /4π) (I.Dl.sinα/r2)
Db = (µ /4π) (I.Dl.sinα/r2)
Where µ = permeability =µ 0. µ r
1/4π is the constant for unit direction and µ0 is constant of free space.
Example of Biot Savart Law
Magnetic Field on the Axis of a Current-Carrying Coil
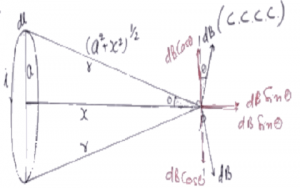
Consider a current ‘i’ is flowing in the current-carrying coil whose circular radius is ‘a’ as shown in the figure. The magnetic field on the axis of a current-carrying coil is found by Biot savart law.
The distance between point ‘P’ and a circular coil central axis is ‘x’. The total magnetic field can be found by considering a small element ‘dl’ on the circular coil.
Magnetic Field on the Axis of a Current-Carrying Coil
The magnetic field at a point ‘P’ is found by using Biot savart law. The circular coil has a radius ‘a’, current ‘i’ is flowing through the coil and axis of the coil is represented by a distance ‘x’ between the point ‘P’.
The magnetic field at this point ‘p’ is to be determined by finding the magnetic field of a small element and integrating it over the complete circular coil.
The expression for flux density on the axis of a current-carrying circular coil (CCCC)
The expression for flux density or magnetic flux induction was derived by Biot and savart and is given as
dB = (I.dl. sinα) /r2
dB at ‘P’ = (µ0/4π ). (i.dl.sin90°)/r2
the angle between ‘dl’ and’ r’ = 90°
dB at ‘P’ =(µ0/4π). (i.dl)/r2
Explanation
- Draw a perpendicular from the first element ‘dl’ to the point ‘P’ which is from the center of the axis of the circular coil.
- Similarly, draw another perpendicular from the second element ‘dl’ to the point ‘P’ which is from the center of the axis of the circular coil.
- The current comes out at ‘dl’ by applying the right-hand rule and the magnetic field will be perpendicular to ‘r’ at point ‘P’. The magnetic field at Point ‘P’ is perpendicular and resolved into two components such as ‘dBcosθ’ and ‘dBsinθ’.
- Similarly, the current due to another element at other parts of the circle is exactly opposite to that of ‘dl’. The current comes out at second element ‘dl’ by applying the right-hand rule and the magnetic field will be perpendicular to ‘r’ at point ‘P’.
- The magnetic field at Point ‘P’ due to the second current element is perpendicular and resolved into two components such as ‘dBcosθ’ and ‘dBsinθ’.
- ‘θ’ is the angle between the point ‘p’ from the center of the axis and perpendicular drawn from ‘dl’ to point ‘P’.
- The radius ‘r’ is calculated by applying Pythagorean Theorem
r = √a2 + x2
where ‘a’ is the radius of the circle `and ‘x’ is the distance from the center of the axis to the point ‘P’.
- At point ‘P’, ‘dbcosθ’ by first element and ‘dbcosθ’ by the second element cancel out each other whereas ‘dbsinθ’ by first element and ‘dbsinθ’ by the second element get added up.
- Therefore, ‘dBcosθ’ by every ‘dl’ will cancel out and every ‘dbsinθ’ by ‘dl’ will be added up.
The Equation for Flux Density on the Axis of a CCCC
The resultant is ∑ dbsinθ I,e summation of ‘dB sinθ’
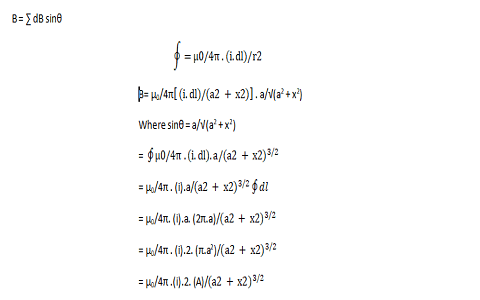
Therefore, If the coil has ‘N’ turns, then
Magnetic field due to a current-carrying coil is given as
![]()
Applications of Biot Savart Law
- It is used to calculate not only magnetic responses at the atomic or molecular level but it can also able to calculate velocity induced in vortex lines by aerodynamic theory.
Know more about Superposition Theorem MCQs.
Thus, in this article, we discussed what is biot savart law, who discovered it, where it can be applied and an example explaining the implementation of biot savart law. Here is a question for the students, what is coulombs law? Compare coulombs law with biot-savart law?