The motor was invented by Michael Faraday who discovered the laws of electromagnetic induction. Actually, the invention began with the discovery of Direct current. This invention led to conduct detailed experiments for the invention of the motor. Earlier direct current was developed in 1800 and further investigations have been made for better utilization of DC. This DC helped in investigating the current supplied to the machine to operate. At the same time, investigations have done on the usage of alternating current. However, for the operation of any machine torque plays a key role. It is the basic twisting phenomenon to rotate the shaft of any machine. We shall discuss the basics of DC motor, how torque is developed, and the derivation of torque and power equation of DC motor.
DC Motor
DC Motor is a type of motor that uses input dc supply and transforms this input electrical energy to the required output mechanical power. The basic DC motor is shown in the figure below.

Basic DC motor
Working
It operates on the law of electromagnetic induction. It also works consistently with the statement made by Lorentz. In accordance with Lorentz, the current-carrying conductor positioned beneath the magnetic field experiences a force. This force enables a unidirectional torque on the conductors which in turn rotates the rotor. The working of a DC motor is shown in the figure below.
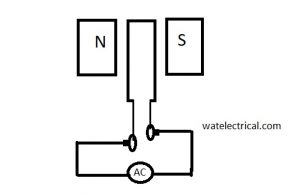
Motor Working
Torque Equation of DC Motor
The equivalent circuit diagram of this type of motor is depicted below.
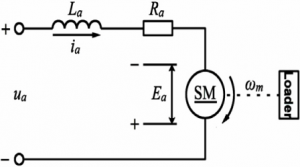
torque diagram
The voltage equation of the motor is given by
V = Eb + Ia Ra
The current equation is expressed as
Ia = V – Eb / Ra
Torque in DC Motor
The torque is defined as the turning moment created at a particular point. The torque at a particular point is explained below.
T = F × R
where,
F is the force acting on the body
R is the radius of the rotor
The speed N at which the force enables to rotate is expressed in rps.
The work done per revolution is given by F × distance covered F × 2πr Joule
Work done per second is given as F × 2πr × N expressed in J/s.
Please refer to this link to know more about DC Motor MCQs
Torque Equation of Permanent Magnet DC Motor Derivation
Torque and Power Equation of DC Motor
The energy generated by the motor is Eb Ia
The mechanical power developed = The electrical power developed
Te 2π N = Eb Ia
Te = Eb Ia / 2π N
The back emf is expressed as below
Eb = N φ Z P / 60 A
Substitute Eb expression in the torque equation
Te = Eb Ia / 2π N
Te = N φ Z P / 60 A / 2π N
Te = (1/ 2π) . (φ Z P / 60 A).
This is the required torque equation that enables the rotor to rotate.
The torque is expressed in N-m. K = (1/ 2π), where K is constant
Te = K. (φ Z P / 60 A).
From the above equation, we can say Te α φ. Ia
Torque Equation for Shunt Motor
The shunt type diagram is explained below.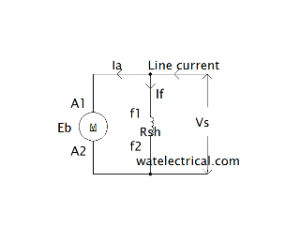
The torque equation of a normal motor is given as Te α φ. Ia
From the diagram, we can observe that φ is constant for a shunt motor as the winding is connected in parallel with the armature.
Torque Equation for Series Motor
The series type diagram is explained below.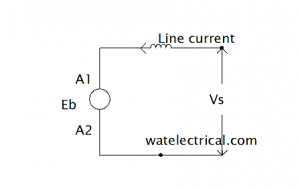
The torque equation of a normal motor is given as Te α φ. Ia
φ α Ia for a series motor as the winding is connected in series with the armature. The torque equation can be written as Te α Ia. Ia
Te α (Ia)2 for a series motor. As the flux is directly proportional to armature current ( φ α Ia ) at a certain point the flux remains constant after its saturation point. In this situation, the Dc series motor acts normal to that of a shunt motor Te α Ia.
Therefore, we had examined the basics of DC motor, how torque is developed. It is basically developed due to the interaction of two forces that creates a unidirectional torque that lets the rotor to rotate. We had also discussed the derivation of torque and power equations. A question to the viewers, how torque is developed in a DC motor?