The Quality Factor ‘Q’ concept was first conceived by an engineer “K. S. Johnson” from the Department of Engineering of Western Electric Company in the United States. He evaluated the quality & performance of different coils. He developed the quality factor concept during his investigation over the course. Surprisingly, his choice of selecting the ‘Q’ letter for the quality factor was made with observation. This concept was applicable in many areas of engineering & physics as a dimensionless parameter that explains how a resonator or an oscillator is underdamped. This article discusses an overview of a quality factor.
What is Quality Factor?
The quality factor can be defined as the ratio of the primary energy of the resonator to the lost energy within a single radian of the oscillation cycle. It is a dimensionless parameter used to describe the underdamped state of a resonator or an oscillator. The working principle of the Q factor is to measure the quality or goodness of a resonant circuit based on its resistance, capacitance & inductance characteristics like its losses & resonator bandwidth. The Q factor is also called voltage magnification because the voltage across the inductor (L) or capacitor (C) within the resonance condition is equivalent to ‘Q’ times the voltage source.
Quality Factor
How to Measure Q Factor?
The Q factor of the radio frequency circuit can be measured by using the Q-meter instrument. This meter helps in measuring the circuit’s Q factor to indicate the whole dissipated energy through the circuit and also the coil & the capacitor characteristics. The Q meter is utilized in a laboratory for measuring the coil’s radio frequency (RF).
Quality Factor Formula
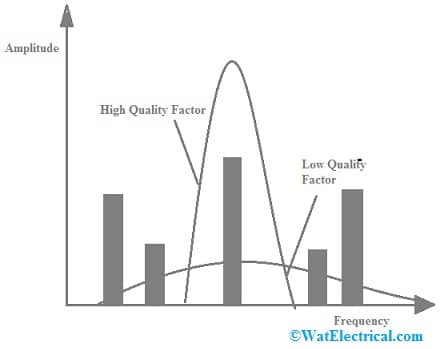
The quality factor of the resonator can be described as the resonator frequency separated by the resonator bandwidth. The formula of Quality factor varies for different electrical circuits.
Q = Resonance Frequency/Bandwidth
Q=fr/BW
Where, ‘fr’ is the resonant frequency, ‘BW’ is the bandwidth frequency & ‘Q’ is the quality factor.
Effects of Q Factor
There are several reasons why the quality factor is significant while dealing with Radio Frequency tuned circuits. Generally, a high level of Quality factor is useful although in some applications, a defined level of QF is necessary. The effects of the quality factor ‘Q’ are discussed below.
Bandwidth
When a Quality factor is increased, then the tuned circuit filter bandwidth is reduced. A tuned circuit becomes very sharper when losses decrease and energy will be stored better within the circuit. The Quality factor enhances, the BW of 3 decibels will decrease & the whole tuned circuit output will be increased. In some situations, a high QF is required to make sure that the relevant amount of selectivity can be attained.
Phase Noise of Oscillator
An oscillator can generate phase noise which includes random changes within the signal process. This manifests as the noise itself that spreads out from the major carrier. It would be predictable; this noise is not preferred and so it has to be reduced.
General Spurious Signals
Filters & tuned circuits are frequently used to eliminate spurious signals. When the filter is sharper & the level of QF is higher, then the circuit is capable of removing the spurious signals.
Ringing
When the quality factor of a resonant circuit enhances, the losses will be reduced which means, any oscillation arrangement in the circuit will tend to ring more. So this is ideal actually to utilize in an oscillator circuit because it is simple to set up & also maintain an oscillation when low energy is lost within the tuned circuit
Quality Factor of Inductor
The Q factor of an inductor can be defined as the ratio of the highest energy stored within the inductor to the dissipated energy for each cycle is given as;
Q Factor = I2XL/I2R => XL/R => ωL/R
Where ‘L’ is the inductance of the inductor & ‘R’ is the resistance of the inductor. Therefore, the Q Factor of an inductor can be given through the inductive reactance divided by the inductor’s resistance.
Quality Factor of Capacitor
The Q factor of a capacitor can be defined as the ratio of the highest stored energy to the dissipated energy within the capacitor within a single cycle is given as;
Q Factor = I2Xc/I2R => Xc/R => 1/ωCR
Where ‘𝑋c’ is the capacitive reactance & ‘R’ is the capacitor’s reactance.
Q Factor of RLC Circuits
The ‘Q’ factor of an ideal series RLC circuit for a TRF or tuned radio frequency receiver is given below.
Q = 1/R√L/C => ω0L/R => 1/ ω0RC.
The tuned circuit’s resistance, capacitance & inductance are R, C & L. Once the resistance of the series is superior, then the quality factor will be lower within the circuit.
The ‘Q’ factor of an ideal parallel RLC circuit is inverse to the series RLC circuit.
Q = R√C/LxR/ω0L => ω0RC.
In an RLC circuit, the resistance, capacitance, and inductance are all parallel.
If the parallel resistance is low, then it will affect more on the circuit damping & the QF is low. So this is very helpful within the design of filtering for the determination of bandwidth.
Quality Factor of LC Circuits
The resistance of the inductor in the parallel LC circuit is in series through the inductance. So this is the main problem within the LC circuit. However, the quality factor is similar to the series circuit. So the QF can be given as;
Q = 1/R√L/C => ω0L/R => 1/ ω0RC.
The resistance, capacitance & inductance of the tuned circuit are R, C & L.
Q Factor and Damping
The Quality factor is normally used for determining the simple damped oscillator’s qualitative performance. The damping within physical systems can be created by processes that dissolve the stored energy within the oscillation.
Overdamped Condition
A system is overdamped whenever the Q factor is <1/2, so it doesn’t oscillate at all, although it displaces from its steady-state output & returns to it through exponential decay by approaching the fixed state value. It has an impulse response that is the amount of two decaying exponential functions with different decay rates.
Once the QF reduces then the slower decay mode will become very stronger relative to the faster mode & controls the response result of the system within a slower system. A second-order LPF with an extremely low-quality factor has an almost first-order step response; the output of the system reacts to a step input by increasing gradually toward an asymptote.
Underdamped Condition
A system is underdamped when the QF is > 1⁄2 which merges oscillation at a particular frequency by a decay of the signal amplitude. Underdamped systems with a low QF may oscillate just one time or above before dying out. Once the QF increases, the relative damping amount decreases. The second-order LPF performance with extremely high QF reacts to a step input by rising above quickly, approximately oscillating & converging eventually to a steady-state value.
Critically Damped Condition
When the quality factor (QF) is intermediate (Q = 1⁄2) then the system is known as critically damped. Similar to an over-damped system, the system o/p doesn’t oscillate really & thus does not exceed its steady-state output. Similar to an underdamped system, the output of this system quickly reacts to a unit step input.
What is the unit of quality factor?
The quality factor (QF) is dimensionless, so it has no SI unit.
What is the use of quality factors?
The use of quality factor is to measure the resonant peak sharpness within a circuit/system. The QF is utilized with various RF-tuned circuits to specify their performance within an oscillator or other type of resonant circuit
What is bandwidth and quality factor?
The quality factor and bandwidth in series RLC circuit are two main factors and the relation between bandwidth and QF in filter circuit is inversely proportional. This circuit needs a high QF because it ensures less energy dissipation & less oscillation damping however high-quality factors can be attained only at the expense of the BW. So, it is necessary to maintain a balance between these two factors according to the necessity.
What is the crankset Q factor?
The q-factor of the crankset is the main distance between the outside of the right and left crank arms.
Thus, this is an overview of the Quality Factor and its effects. The Quality factor is a key aspect of filter & resonant circuits, particularly in RF design and also in other areas like electronic circuit design. Here is a question for you, why Q factor is significant?