Intensity basically defines the strength of the source like light intensity, which defines the luminosity of light source, electromagnetic field intensity defines the strength of the magnetic field. Similarly, electric field intensity defines the strength of the electric field. This is a vector quantity, which basically means force per unit charge. This parameter is extensively used in the field of electromagnetics, electrostatics, high voltage engineering, etc. for the design of equipment like insulators, antennas, etc. It is also evaluated as the performance parameters of electric machines and many electronics equipment. This is majorly used to evaluate whether the electric field is stronger or weaker.
What is Electric Field Intensity?
Definition: Electric field intensity is the force that is experienced by a unit positive charge which when placed in an electric field. It is a vector quantity since it has both magnitude and direction. It is used while calculating the intensity of electric fields, which is used while designing and analyzing the equipment’s performance. A field is a function that specifies a particular quantity everywhere in a region.
Mathematically the formula of electric field intensity can be expressed as
electric-field-intensity-formula
In the above eq(1), Where ‘E’ is electric field intensity, ‘F’ is the force existing between two point charges and ‘Q’ is the point charge.
How to Calculate Electric Field Intensity?
To calculate this first, we need to evaluate the force between two charges. As per coulomb’s law, the force between two charges Q1 and Q2 can be defined as
F = KQ1Q2/R2
In the above equation(2), Q1 and Q2 are two point charges and ‘R’ is the distance between the point charges. By point charge, it is meant that collection of charges (electrons) at one point. Electrons are regarded as point charges and the polarity of the charges may be positive or negative. The charges are measured in Coulombs where one Coulomb is approximately equal to 6 X 1018 electrons. Also, one electron charge can be expressed as e= -1.6019 X 10-19 C. In the equation, k is the constant whose value is equal to k= 1⁄4πϵ0. In the expression, ‘ϵ0’ is known as permittivity of free space and has a value of 8.854 X 10-12.
From equation (2) it can be seen that the force is directly proportional to the product of charges and inversely proportional to the square of the distance between them. A generalized expression for force is needed to evaluate intensity.
Consider the following figure
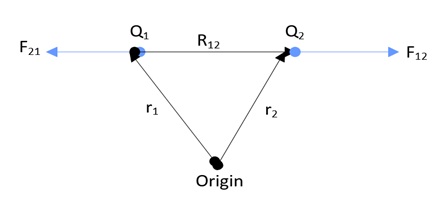
electric-field-intensity-force-on-the-point-charges
In the above fig, two-point charges Q12 and Q21 are shown. R12 is the distance between them and r1, r2 are the position vectors along with origin. F12 is the force exerted on Q2 due to Q1 and similarly F21 is the force exerted on Q1 due to Q2.
The equation (2) now can be modified as
F = Q1Q2/ 4πϵ0R2
Considering the position vectors r1 and r2, equation (3) can be modified as
![]()
Where,
Substituting the above, we get the equation (5) for force as
F12 = (Q1Q2/ 4πϵ0R3) R12
Once we get the equation for force, now the intensity can be defined as
![]()
Or in simple words, E= F/Q
From the above equation (6), it can be seen that, for a value of Q greater than 0 i.e. Q>0, the intensity is in the direction of the Force ‘F’ and is measured in newtons per coulomb, or volts per meter.
Hence the unit of electric field intensity if newtons per coulomb or volts per meter.
Substituting the values of Force from equation (5) in equation (6) an expression for electric field intensity can be obtained as
![]()
Where ‘E’ is the electric field intensity at point ‘r’ due to point charge ‘Q’. For ‘N’ number of point charges the electric field can be generalized as E = E1+E2+E3+….EN or ![]()
The above equation expresses electric field intensity for ‘N’ point charges (Q1, Q2… Qn) located at r1, r2,.. rn. Hence based on the value of point charges, location of charges, position vectors, etc, the intensity can be evaluated. Since based on the value of charge, the direction of the electric field is evaluated, and based on the number of charges present in a particular field, the magnitude of the electric field is calculated.
Since the electric field intensity has both magnitude and direction, it is considered as a vector quantity. Other vector quantities include velocity, force, momentum, acceleration, displacement, etc. On the other hand, the scalar is the quantity that has the only magnitude like mass, temperature, electric potential, etc.
As mentioned, this is one of the important parameters for the design and performance analysis for many electric and electronic equipment like overhead line insulators (high voltage engineering) and antennas (microwaves), etc.
The Dimension of Electric Field Intensity
From the above equations, we have seen that electric field intensity is defined as force per unit charge. Now the dimensions of force are kg-m-2 or MLT-2. The dimensions of coulomb are ampere-sec or AT. So the dimensions of this become MLT-3A-1.
We have evaluated this based on Coulomb’s law. Similarly, it can be also evaluated based on Gauss Law. In fact, it is easy to use Gauss Law, since the charge distribution is uniform which is not the case for Coulomb’s Law.
The fundamental relation between electric field intensity and electric flux density can be expressed as
D= ϵ0 E
Where ‘ϵ0′ is the permittivity of free space and ‘E’ is the electric field intensity.
If we consider the electric field strength, it is very strong as compared to the gravitational field. However, the magnetic field is far stronger than the electric field.
FAQs
1). Is force a vector?
Yes, force is vector since it has both magnitude and direction. Other examples of vector quantities are velocity, acceleration, etc.
2). What is the Electric field strength?
It can be defined as the magnitude of the electric field which is produced by point charges with a certain charge. The charge is defined in terms of coulombs.
3). Is electric Field a vector field?
Ans. Yes, since the electric field has both magnitude and direction, it can be classified as a vector field. Other examples of a vector field are velocity, force, acceleration, etc.
4). Who discovered Electric Fields?
Ans. In 1820, a Danish scientist named Hans Christian Oersted discovered that electric current produces a magnetic field. In 1830, Michael Faraday proved that the opposite is also true that a magnetic field can be produced by electric current. Hence came the concept of electric field and electric field intensity
5). Is an electric field a force?
Yes, the electric field is force per unit charge. It’s a vector quantity with both magnitude and direction.
Know more about Electric Flux MCQs.
Thus, this is all about an overview of electric field intensity, We have seen how it is defined as force per unit charge and can be calculated for any ‘n’ number of charges. On simplification, it can be observed that the intensity equation depends only on charge ‘Q’ and permittivity medium. Once electric field intensity is evaluated, we can calculate electric field density which is one of the important parameters for design aspects. It is frequently used in the field of electromagnetics and high voltage engineering. Here is a question for you, what is electric field density?