For inductor-coupled circuits, the coefficient of coupling is a significant factor to decide the amount of coupling between the inductively coupled coils. These coils are coupled with the magnetic flux. If one inductor’s total magnetic flux is coupled with the other inductor then it is known as perfect coupling. In this situation, this coupling (K) is expressed as 1 which means 100% coupling. The mutual inductance mainly depends on the coefficient of coupling between the two inductively coupled coils. If this coupling is higher, then it will increase the mutual inductance within the coupling circuit. Similarly, if this coupling is lower then it will decrease the mutual inductance within the coupling circuit. This article discusses an overview of the coefficient of coupling.
What is the Coefficient of Coupling?
The coefficient of coupling definition is; the fraction of the generated magnetic field through the current within a single coil that connects with another coil. It is signified simply by the ‘k’ symbol. The sum of coupling between two inductively coupled coils can be expressed in terms of the coefficient of coupling.
The value of this coupling cannot be a negative number & it doesn’t depend on the current flow direction in the coils but it mainly depends on the core materials like ferrite or iron. So the coupling coefficient for these materials will be extremely high like 0.99 & it is low for the air core that ranges from 0.4 to 0.8 based on the space in between the two coils.
Coefficient of Coupling Derivation
The coefficient of coupling provides the communication between two inductor coils which is known as mutual induction. This is the main property of two inductor coils where each coil resists any change within the strength of the current in another coil because of induced emf. The mutual inductance among the two coils will be the same. An inductor is an electronic component that includes two terminals that store energy within the magnetic field once electric current is supplied throughout it. The coefficient of coupling between two coils is discussed below.
The coefficient of coupling between two coils or an inductor is shown below.
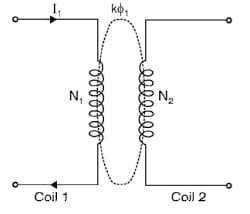
Coefficient of Coupling
In the above diagram, there are two coils that are magnetically coupled with turns N1 & N2 correspondingly. If the ‘I1’ current flows in the first coil then it generates ϕ1 magnetic flux with N1 turns, then the self-induction of the coils is given as
L1=N1ϕ1/I1 —-(1)
Suppose the coupling between two coils is ‘k’ then ‘kϕ1’ signifies the magnetic flux coupled with the second coil after that the mutual inductance within the first coil because of the second coil can be given as;
M12=kϕ1N2/I1 —-(2)
When the current ‘I2’ is flowing in the second coil then it will generate ϕ2 magnetic flux with several N2 turns, then the self-induction of the coils will be given as;
L2 = kϕ2N2/I2 —-(3)
Suppose, the coupling between two coils is ‘k’ then ‘kϕ2’ signifies the magnetic flux coupled with the first coil after that the mutual inductance within the second coil because of the first coil can be given as;
M21=kϕ2N1/I2 —-(4)
By multiplying equations 2 & 4, we can get
M12×M21= (kϕ1N2/I1)×(kϕ2N1/I2) —-(5)
We know that the mutual inductance between two coils will be equivalent. thus,
M12 = M21
Now equation 5 will become
M^2=k^2(ϕ1N1/I1)×(ϕ2N2/I2)
From the above equation1 & equation3, L1= ϕ1N1/I1 & L2 = ϕ2N2/I2.
M^2=k^2L1L2
k^2=M^2/L1L2
The formula of coefficient of coupling k= M/√ L1L2.
Where,
‘M’ is the mutual inductance between two coils.
‘L1’ is the first coil’s self-induction.
‘L2’ is the second coil’s self-induction.
Example
Find out the coupling coefficient when two inductor coils are connected in a series with 200 mH total inductance. When these inductors are connected in a series-opposing arrangement, then the total inductance of coils is 120 mH. If one coil’s inductance (L1) is 3 times the other (L2), then what are the values of L1, L2, & M.?
L1 +L2 + 2M = 200 —-(1)
L1 +L2 – 2M =120—–(2)
Add the above 1 & 2 equations, then
2L1 +2L2 = 320
2 (L1 +L2) =320 => L1 + L2 = 160 —–(3)
We know that L1 is three times to L2, so
L1= 3L2 —–(4)
By substituting equation 4 in equation 3, then we get
L1 +L2 =160
3L2 +L2 =160 => 4L2 = 160 => 40
L2 =40 mH
By substituting this L2 value in the above equation we get L1.
L1 +L2 =160
L1 +40 =160
L1 = 120 mH
We know that, L1 +L2 + 2M = 200
120+40+2M =200
160+2M = 200
2M = 40
M= 20 mH
We know that k= M/√ L1L2.
Substitute M, L1 & L2 values to get the ‘K’ value.
K = 20//√120×40 =>20/√4800
K = 20//69.28 = 0.288
What is the Maximum Coefficient of Coupling?
The coefficient of coupling is always less than ‘1’ & its highest value is ‘1’only. If the value of this coupling is one, then it is the perfect coupling so, once the total flux of a single coil connects the other. If the coefficient of coupling between two inductors is higher then their mutual inductance is also greater.
What is K in Coupling?
The coefficient of coupling is represented with the symbol ‘k’.
What is the Piezoelectric Coupling Factor?
The piezoelectric coupling factor (k^2) can be defined as the ratio of the converted & the supplied energy. So this factor is considered frequently as a measure of the material’s transduction efficiency.
What is the Minimum Value of the Coefficient of Coupling?
The minimum value of the coefficient of coupling is always less than 1.
What is the Coupling Factor in Transformer?
The coupling factor of the ideal transformer is equivalent to 1.
Know more about Magnetic Circuit MCQs, Magnetic Materials MCQs.
Thus, this is an overview of the coupling coefficient or coefficient of coupling and its derivation. This coupling provides the flux information which is coupled between two coils. So, if ‘K’ is 1 then flux linkage is high and if ‘K’ is 0 then flux linkage is low. So this coupling value ranges between 0 & 1. Here is a question for you. An inductor is also called an?