In the domain of electronics and electromagnetism industries, inductance is the movement of the electrical conductor to obstruct the flow of current. The current movement develops a magnetic field across the conductor and this field strength is based on the current magnitude and any current variations. From the principle of Faraday’s law of induction, any deviation in the magnetic field along the circuit generates an EMF voltage and this is termed as electromagnetic induction. And this induced voltage directs to obstruct the path of current flow and this is defined as back EMF. As because of this, the inductance of the conductor resists electric current that flows through it. So, this theory stands as a base for the concept of self-inductance. Let us discuss this concept in more detail.
What is Self Inductance?
Self-inductance is the force that is observed when a coil undergoes an inductance effect. In other terms, it is defined as the property of the coil which obstructs the current flow that passes through it. Inductance is achieved by the coil because of the self-developed emf that is generated in the coil by altering the flow of current through it. The basic self-inductance theory is explained as that when there is a current passage across the wire, mainly through either inductor or coil, there will be the development of the magnetic field. This field is extended from inductor or wire and possibly linked up with other circuits. Even it will be also linked up with the circuit from which it is constructed.
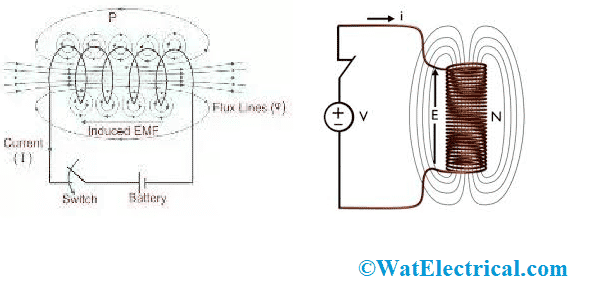
Self Inductance And Output
The developed magnetic field is also observed as concentric circles of magnetic flux that encircle the wire and the larger loops combine with other loops of the coil which facilitates self-inductance in the coil itself. When there is a change in the current that flows across the coil, the voltage will be developed in various loops of the coil which is self-inductance.
Derivation of Self Inductance
Basically, self-inductance is also termed as the proportion of developed EMF along with the coil to the amount of current change in the coil. Through this definition, this concept can be easily derived. As the developed EMF has direct proportion to the current change
E α (di/dt) = E = L (di/dt)
Where L = E/(di/dt)
Here ‘L’ corresponds to inductance
This is actually represented as E = -L*(di/dt)
For a DC circuit, when the switch is in ON state which means when t is at ‘0’, there will be current movement from ‘0’ to a specific value in correspondence with time. This creates an amount of change in current steadily and this develops flux change across the coil. This condition is shown as dϕ/dt.
Now, with the application of Faraday’s law,
E = N.(dФ/dt)
Where ‘N’ corresponds to the number of coil turns and e is the generated EMF. Upon the application of Lenz’s law in the above equation, we get
E = -N*(dФ/dt)
To know the inductance value, the above equation is modified as
E = -N*(dФ/dt) = E = -L*(di/dt)
Where N dФ = L.di
=> NФ = Li
As a result, NФ = Li = NBA
Here ‘B’ corresponds to flux density which is B = ϕ/A
‘A’ corresponds to the coil’s area
Nϕ or Li is termed as magnetic flux connection and represented as Ѱ.
As Hl = Ni, ‘H’ corresponds to magnetizing strength which is because of magnetic flux lines movement from the south pole to north internal to the coil. Also, B = µH
Li = NBA which implies L = (NBA/i) = (N2BA)/Ni
- (N2µHA)/Hi [As B= µH and Ni = HI]
- L = µN2A/l = µN2∏r2/l
This is the self-inductance formula and the SI unit of self-inductance is Henry represented as H.
The relation between Self-inductance and Mutual Inductance
In self-inductance, the alteration in the current strength of the coil is obstructed by the coil itself with the induction of EMF. While in mutual inductance, from the two coils one coil obstructs the current strength that flows in the other coil.
With the below derivation, the relation between self and mutual inductances can be known.
Let us consider the coil turns is N1, l is the length and A is the cross-sectional area of the primary coil. When there is flow of current through the coil, then the magnetic flux association is
Ф = lµ0N12lA
Where the inductance of the primary coil is L1 = IФ1 => lµN12A. And the self-inductance of the secondary coil is
L2 = lµN22A
When there is current flow through P, then the flux linkage across S is
Ф0 = lµ0N1I *N2A
So, the mutual inductance of both the coils is
M = IФs
From the above equations, L1*L2 = lµ0N1N2A. When this equation is compared with the mutual inductance, the final equation is
M = L1*L2
There are a few factors affecting self-inductance. With the effect of these factors, the output performance and efficiency get changed. And the factors are:
- The self-inductance is more when there is a strong magnetic flux for the provided value of the current
- Self-inductance is also based on the core material, the number of turns presents either in the solenoid or coil
- As self-inductance is measured in Henry, the higher the value of Henry, the change in current rate will be minimal (1 Henry corresponds to 1Weber/ampere)
These are the main factors showing impact.
Examples
1). When a solenoid has 900 turns with a flux value of 1.33 ×10-7 Wb and the current across the coil is 100mA. When the time taken by the flux to move from ‘0’ to the maximum level is 76 ms, then measure the coil’s inductance. Furthermore, know the counter EMF generated in the coil at the time of flux generation?
Ans: Given that
Δϕ=1.33×10−7Wb
Δi=100 mA
Δt=75 ms
From the formula L = N (Δϕ/Δi)
= 900 [(1.33×10−7)/( 100×10−3)] = 1.2mH
And eL = 900 [(1.33×10−7)/( 75×10−3)] = 1.6mH
2). When a coil of 50 turns generates an EMF of 2.0V at the time when the current flow through the coil raises consistently from 0.0 to 5.0 Amps in 0.10 sec. Then
-
- Calculate the coil’s self-inductance
- When a current of 5.0 Amps flows through the coil, what is the amount of flux generated across each coil turn?
Ans : We know the formula that
L = є (dI/dt) = 2.0 / (5.0 × 0.10)
= 4.0 × 10-2 H
This is the self inductance of the coil
Also, we know Фm = LI/N
Фm = [(4.0 × 10-2) (5.0)]/(50 turns)
= 4.0 × 10-3 Wb
So, these are basic examples of self inductance
Know more about Electromagnetic Field Theory MCQs, Magnetism and Electromagnetism MCQs.
On the whole, this is a detailed theory. This article has clearly explained on the concepts of definition, SI units, how the formula is derived, the relation between self and mutual inductance, and its examples. In addition, it is more important to know about the concepts of applications of self-inductance, how the dimension of self-inductance and dimensional formula of self-inductance is derived?