To know the detailed analysis behind the Carey foster bridge circuit, initially, it is more crucial to know basically about what a bridge circuit is. A bridge circuit is an electrical circuit where the branches of two circuits are connected by the third branch and it is bridged in between the first two circuit branches at the intermediary location across them. The main purpose of bridge circuits is for laboratory calculations. Now, these circuits are widely implemented in many applications, and there comes much enhancement in the design and construction of bridge circuits. This led to the development of many kinds of bridges such as Wheatstone, Maxwell, Wien, Fontana, kelvin, lattice, Carey foster, and many others. So, today the main discussion of ours is on “Carey Foster Bridge”. The below theory explains clearly the principle, circuit, its calibration, and uses.
What is Carey Foster Bridge?
In the domain of electronics, the main use of the Carey foster bridge is for the calculation of medium resistance values or to know minimal variations that exist between high resistance values. This bridge is termed as the modification of the Wheatstone bridge. It was developed by Carey Foster in the year 1872 and the bridge name itself indicates the creator name.
Circuit Diagram
The Carey foster bridge circuit below explains how the bridge is constructed. The constructional set up of this device is classified into two sections
- Bridge arrangement
- Testing section – This unit is included with power supply, galvanometer, and variable resistances. Here Dc supply is used because it eliminates the complication of battery discharge in correspondence to the time where it shows an impact on the output.
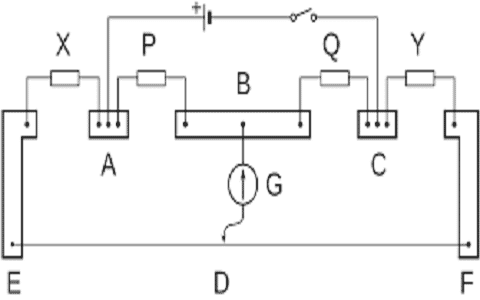
Construction Of Carey Foster
Here, ‘A’ and ‘B’ are the known resistances were used for the comparison. While ‘C’ and ‘D’ are the two similar resistances so that one half of the bridge is constructed with these. The wire ‘PQ’ includes a jockey contact ‘O’ that is positioned across it and it has a movement till the galvanometer reading shows ‘0’. The wide fringed areas have dense copper bush bars that measure the resistance of ‘0’.
- Place the unknown and known resistances at the position’s ‘A’ and ‘B’.
- Alter the position of ‘O’ across the wire so that the galvanometer records zero.
- The distance from P and Q is measured as ‘l1’.
- Alter the positions of ‘A’ and ‘B’ and then again adjust the position of ‘O’, so that again the galvanometer reading is zero. Here, the distance between PQ is taken as ‘l2’.
For the initial balanced condition, the equation is
A/B = (C + l1r)/( D + [L- l1] r)
Here ‘r’ represents resistance calculated across the length of the wire.
When the positions of C and D are changed, then the balanced equation is
A/B = (D + l2r)/( C+ [L- l2])
From the initial balanced equation, we get
(A/B) + 1 = [C + l1r + D + (L- l1) r]/[ D + [L- l1] r]
= [C + l1r + D]/[ D + (L- l1) r]
And from the second balanced equation, we get
(A/B) + 1 = [D+ l2r+ C+ (L- l1)r]/[ C+ (L- l2)r]
From the above two equations,
(A/B) + 1 = [C+D+Lr]/[ C+ (L- l2)r]
So, D + (L- l2) r = C + (L- l1) r
D-C = (l1– l2)
When the wire’s resistance is calculated as ‘σ’ in terms of percentage, then the resistance variation is defined as the resistance of the wire length measured between ‘l1’ and ‘l2’. This bridge shows enhanced sensitivity when all the resistance such as ‘A’, ‘B’, ‘C’, and ‘D’ have equivalent magnitude values.
Calibration of Slide Wire
The slide wire calibration can be known by positioning the unknown resistances ‘C’ and ‘D’ in the parallel side with the siding wire of the known resistance’s ‘A’ and ‘B’. Let us consider that D is the known value and D’ is the value when it is shunted by the known value of resistance. Then
D-C = (l1– l2)r and D’-C = (l1’– l2’)r
[D-C]/ (l1– l2) = [D’-C]/[ (l1’– l2’)]
The final equation after computing the above equation is that
C = D[(l1’– l2’) – C(l1– l2)] /[(l1’– l2’ – l1 + l2]
So, with the assistance of the Carey foster bridge, the direct relation that exists between the unknown resistance’s length can be measure. The resistance value of other equipment such as for A, B, and the sliding wire O can be totally neglected.
So, this is how the calibration of the sliding wire through the Carey foster bridge can be measured.
Errors
Upon the connection of this bridge, there might be the chance of arising errors and those are

Detailed View
- Sometimes, the edges of the connection wires, copper strips, and the tip ends of the resistance box are not clean and this results in excessive contact resistance at the connecting points.
- Even the plugs that are connected to the fractional resistance box might be not tight thus developing adverse contact resistance.
- There might be the chances of sliding wire getting heated because of an uninterrupted flow of current through the wire for a long period which leads to a change in resistance value
- When the jockey is not tightly connected or when it is pressed hard on the wire, or else at the time of wire being transferred from one place to another, this will modify the cross-sectional dimension of the wire and makes non-uniformity in the wire.
Advantages of Carey Foster Bridge
A few of the advantages of this bridge are as follows:
- The bridge delivers enhanced accuracy because effective wire length can be augmented by forming a series connection with every wire edge.
- No additional equipment is required other than a sliding wire and resistances. This reduces the circuit complexity
Applications
The applications of Carey foster bridge are
- It is used in applications where medium resistance values are to be measured
- Employed for the purpose of comparing almost similar valued resistances
- Carey foster bridge is used to know the exact value of resistance of a wire
Know more about AC Bridge MCQs, Schering Bridge MCQs.
Finally, this is all about the Carey foster bridge which can be developed just by using simple apparatus. With its simple construction, design, and advantages, this bridge can be easily implemented in various applications in multiple domains. As because of its importance and wide implementation, it is more recommended to also know about a few examples of Carey foster bridge and how it is different from Wheatstone bridge?