As we are in the era of digital technology, the foremost concept to be known about is electronic engineering. As every industry in this digital scope needs of electronic instruments, one has to be clearly aware of its concepts and properties. The one concept which we are going to discuss is the temperature coefficient of resistance. When there is current movement through the wire, heat gets generated through this because of resistance in the wire. This scenario stands as the fundamental principle of this concept. Let’s move ahead and discuss on TCR and its formula, definition and related units.
What is the Temperature Coefficient of Resistance?
The temperature coefficient of resistance which is briefly termed as TCR is defined as the variation in electrical resistance of the substance in correspondence with the variation in temperature. It has to be noted that the resistivity of materials varies with temperature because of two reasons.
- One is because of collisions between electrons and holes in the substance. The change in temperature will parallelly change the resistivity values and so the collision rate too.
- The other is a decrease in temperature with the enhancement in resistance values, which is most common in semiconductor materials.
When observing at the temperature and resistance values, it can be understood that the TCR graph will be a linear shape. This is the graphical representation of both metals and similar types of substances. It is also known that change in resistance depending on collisions is not continually steady especially at very minimal temperatures for these metals. The average free path in between the collisions of charge carriers varies inversely with the resistance levels. For the temperatures of more than 150K, this is confined by atomic thermal vibrations which are in the form of linear shape. In minimal to these temperature ranges, resistivity values are confined by charge carriers and few contaminations.
The temperature coefficient of the resistance formula can be known by the below equation and it is
R = Rref (1+α(T-Tref))
In the above formula,
‘T’ corresponds to operating temperature calculated in Celsius
‘R’ is the resistance at the operating temperature
‘α’ represents the material’s TCR
Tref is the reference temperature where the TCR is quantified
TCR value is normally standardized at the temperature range of 200C which is generally at room temperature and the formula for TCR at room temperature is represented as:
R = R20(1+α20(T-20))
And in the above formula ‘R20’ is the resistance value calculated at 200C temperature and
‘α20’ corresponds to TCR value at 200C
The SI unit of temperature coefficient of resistance is represented as per degree Celsius which is /0C
Define Temperature Coefficient of Resistivity
The temperature effect is not only on resistance but also on the resistivity of the materials. In the scenario of conductor substances, there will be a linear increment in both the parameters (that is directly proportional). So, the technical definition of the temperature coefficient of resistivity is the rate of variation in resistivity in correspondence with degree variation in temperature. At normal temperature changes, these parameters vary linearly, while in the situations of too minimal and extremely high temperatures, the parameters are non-linearly related.
The formula for temperature coefficient of resistivity is given by
ρ = (ρ2 – ρ1)/(t2 – t1)
where ‘ρ1’ is the conductor resistivity calculated at t10 temperature
‘ρ2’ is the conductor resistivity calculated at t20 temperature
In many of the situations, the values of the temperature coefficient of resistance of temperature coefficient of resistivity are generally equal.
Temperature coefficient of resistance is categorized as two
- Positive TCR
- Negative TCR
Positive Temperature Coefficient of Resistance
PTC corresponds to the increase in the material’s resistance when the temperature values are increased. Mostly, industrial materials exhibit a positive temperature coefficient of resistance which means an increased coefficient. The more coefficient values, the more material exhibit resistance values. PTC materials are designed to get to increased temperature values for the specified voltage levels because any additional increment in the temperature can reach to maximized resistance values. PTC materials are fundamentally self-restricting materials. PTC rubber is an example of a positive temperature coefficient of resistance.
Negative Temperature Coefficient of Resistance
NTC corresponds to the decrease in the material’s resistance when the temperature values are increased. Mostly, engineering materials exhibit a negative temperature coefficient of resistance which means minimal coefficient values. NTC materials are designed to get to decreased temperature values for the specified voltage levels because any additional increment in the temperature can reach to maximized resistance values. These materials are utilized for the creation of inrush current regulators because the reason they exhibit maximum initial resistance values till the current specification limit reaches to quiescent value. Examples of these materials are thermistors and a few kinds of sensor devices.
The temperature coefficient of resistance of metals like copper, platinum, and others at 200C can be known through the below table:
| Material | Alloy or Element | TCR value in Celsius |
| Iron | Element | 0.005671 |
| Tungsten | Element | 0.004403 |
| Aluminum | Element | 0.004308 |
| Copper | Element | 0.004041 |
| Silver | Element | 0.003819 |
| Gold | Element | 0.003715 |
| Zinc | Element | 0.003847 |
| Molybdenum | Element | 0.004579 |
| Nickel | Element | 0.005866 |
| Platinum | Element | 0.003729 |
| Constantan | Alloy | -0.000074 |
| Nichrome V | Alloy | 0.00013 |
| Nichrome | Alloy | 0.00017 |
| Steel | Alloy | 0.003 |
| Manganin | Alloy | +/-0.000015 |
Experiment
Below is the temperature coefficient of resistance experiment
Objective
This experiment is done to know the TCR of coil
Required Equipment
- A resistor with low value
- Galvanometer
- Wires
- Carey foster bridge
- Resistance box
- Accumulator made of lead
Hypothesis
Here, a Carey foster bridge is connected in the same way as that of meter bridge where four resistors named with A, B, C and X are connected to each one. The connection diagram is shown as below:
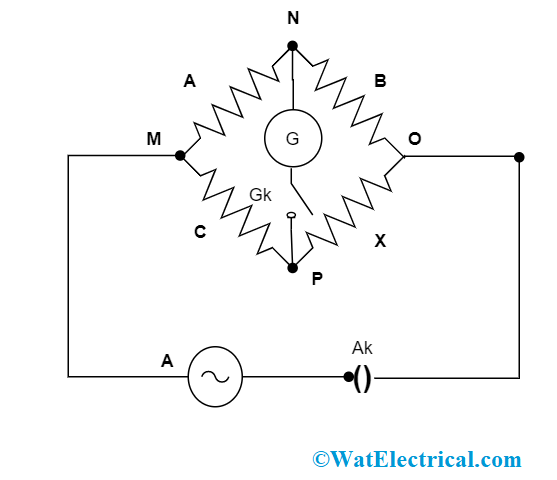
Wheatstone Bridge to Calculate Temperature Coefficient of Temperature
In the above diagram,
‘G’ corresponds to Galvanometer,
‘A’ corresponds to Accumulator,
‘Gk’ and ‘Ak’ corresponds to Galvanometer key and accumulator keys
When there happens any change in the resistance values, the galvanometer shows current value as ‘0’ and the values of any three resistors in A, B, C and X are known, then the other can be known automatically where
A/B = C/X
Carey foster bridge is utilized in the circuit to calculate the variation that exists between two almost similar resistances by knowing one value, the other can be measured. The end resistance values are not considered.
Method of Calculation
Assume ‘A’ and ‘B’ are the identical resistances that are connected in between the gaps 2 and 3, ‘C’ is positioned at gap 1 and X is positioned at gap 4. The length between E and D is considered as l1 and through whetstone’s theory,
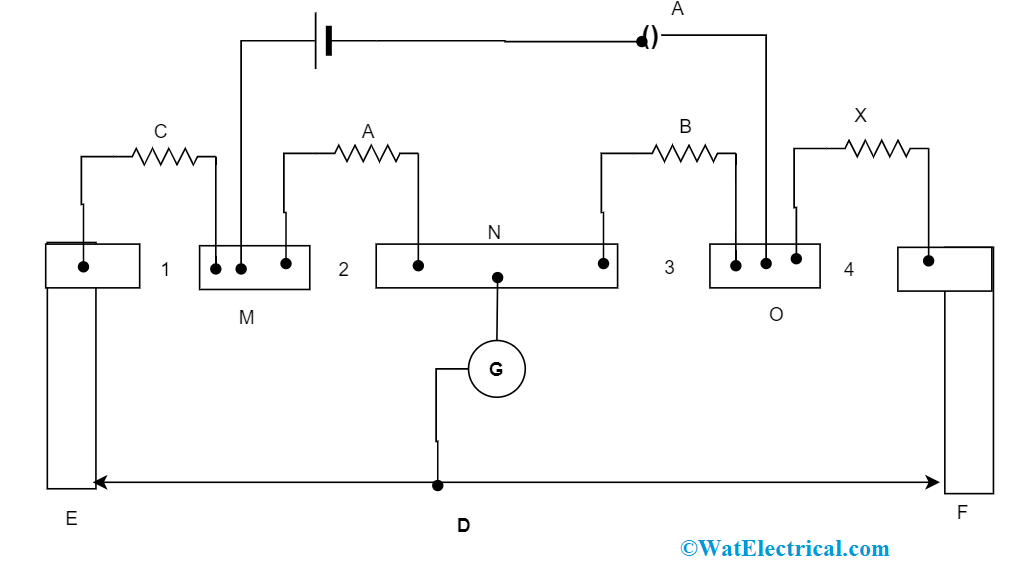
Carey Foster Bridge
A/B = (C+a+l1ρ)/(X+b+(100-l1)ρ) ———(1)
Here ‘a’ and ‘b’ are the edge corrections at the edge E whereas F corresponds to the resistance of the bridge wire length.
When the experiment is done when X and C are swapped, and l2 corresponds to balanced length then,
A/B = (X+a+l2ρ)/(C+b+(100-l2ρ) ——-(2)
From the above two equations
X = C + ρ(l1 – l2) ——–(3)
And assume that l1’ and l2’ are the balancing lengths when the experiment is carried out with standard resistor which has r = 0.1 and C is replaced by copper strip having ‘0’ resistor then
0 = r + ρ(l1’ – l2’)
When the coil resistance values are measured at temperatures 00 and 1000 C then
Α = (X100 – X0)/ (X0 × X100)
FAQs
1). How does temperature affect the resistance?
When the temperature increases, resistance increases as electrons accumulate energy with the heat enhancement and happens more collisions between the electrons.
2). What is the temperature coefficient of resistance of a semiconductor?
In most of the cases, the TCR value of semiconductor is zero
3). What is Ohm’s law used for?
Ohm’s law is used to know the relation between the voltage, resistance and current levels in the circuit.
4). What is the SI unit of specific resistance?
Ohm is the unit of specific resistance
5). What is the low-temperature coefficient of resistance?
It corresponds to a decrease in temperature values when the resistance values are increased.
So, this is all about the concept temperature coefficient of resistance. Finally, we can summarize that there is a close relationship between the temperature and resistance levels either they are directly or indirectly related to the cases of metals or semiconductors. The other concepts to be known are what is the temperature coefficient of resistance derivation and a few sample problems regarding this?