The transformer is the most prominent passive device that has the operation of transferring electrical energy from one circuit to another, it is used in various applications across multiple domains. Also, there are a wide variety of transformer designs in electrical and electronic domains, every type encounters various types of losses in transformer.
So, it is even more crucial to know the types of losses in the transformer and how these losses show an impact on the performance of the transformer. And this article gives a clear and detailed explanation of what are the losses in a transformer like Iron losses, Hysteresis, Stray, dielectric losses, and others.
What are the Types of Losses in a Transformer?
In any type of electrical device, a loss is stated as the difference that is between input and output power. The losses in the transformer are the same as DC machine losses except in the scenario that transformers do not possess mechanical type losses. The losses in the device are generated by the flow of current and altering magnetic field in the core and these are termed as load losses, while the losses generated in the core section are termed as no-load losses. Even though there are no mechanical losses in the device, there exist electrical losses.
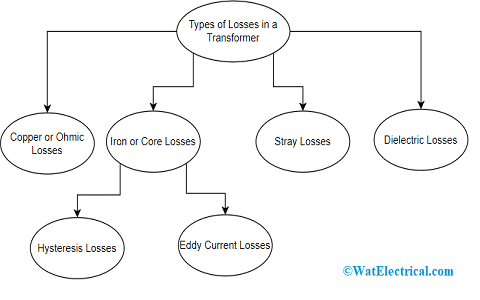
Types of Losses in a Transformer
The main and primary types of losses in a transformer are copper and iron losses.
Copper Losses
These are also termed ohmic losses. The losses occur in the transformer winding when there is heat dissipation because of the current flow across windings and internal resistance in the windings. Because of this, the losses are termed as I2R losses, where ‘I’ represents the current flow and ‘R’ represents resistance across windings. As the losses are present in both the windings and it is based on the load connected all through the secondary windings because there exists current variation as per load and so the losses are also called as variable losses.
In a mathematical form, the copper losses are represented as below:
Pcopper = Ip.Rp + Is. Rs
Where ‘Ip’ and ‘Is’ corresponds to current flow across primary and secondary windings
And ‘Rp’ and ‘Rs’ are the resistance of primary and secondary windings
As Ip.Tp = Is.Ts
Ip = Is. (Ts/Tp)
So, Pcopper = Is. (Ts/Tp). Rp + Is Rs
This implies that copper loss varies corresponding to load current.
Finally, Pcopper = IpRe1 = Is. Re2
Iron Losses
These iron losses tool place in the transformer’s core section and these are produced because of the flux variations. These are dependent on the substance magnetic properties that exist in the core section and so the losses are called iron losses which correspond that the transformer’s core section is formed with iron substance. Also, these losses will not vary like load, so these are constant.
Iron losses are further categorized as hysteresis and eddy current losses. So, let’s discuss further on these losses.
Hysteresis Losses
These losses are defined as the electrical energy that is necessary for rearranging the spheres of ferromagnetic substance that exist in the transformer’s core section.
The spheres of the substance fail to have their rearrangement when an AC current is allowed to flow through the transformer’s primary windings, and this induces an EMF in the ferromagnetic substance that interrupts the arrangement, and later they will not come back to their original realignment state. To get back their exact rearrangement, an additional energy supply such as current is needed and this additional energy is termed hysteresis loss.
In mathematical representation, these losses are given as below:
Phystresis = KhBmxfV
Here ‘Kh’ is a constant term that is directly proportional to used units, size of the core substance, and volume.
‘Bm’ is the maximum amount of flux density of the core substance
‘f’ represents the frequency of the variable flux
The exponential term ‘x’ Steinmetz constant. It varies depending on the core substance magnetic properties and varies between 1.5 – 2.5
Eddy Current Losses in Transformer
When there is the supply of AC current to the transformer’s primary windings, this results in the generation of varying magnetic flux inside the winding and then this flux gets induced in the secondary winding of the transformer. This happens because of Faraday’s principle of electromagnetic induction. From the secondary winding, the flux transfers to the external load section. At this condition, the other conduction components that are present in the core section also get connected with this varying flus and induces EMF.
But this varying magnetic flux does not show any impact either on the external load or output power and it gets dispersed in the form of heat. Because of this, the losses are termed as eddy current losses and are represented as follows:
Peddy = Kef2Kf2Bmax2
In the above equation,
‘Ke’ represents the constant term of eddy current
‘Kf’ represents the constant term of form factor
‘Bmax’ corresponds to the capability of magnetic field
Based on the above hysteresis and eddy current losses, the iron loss is represented as
Piron = Physeresis + Peddy
So, Piron = KhBmxfV + Kef2Kf2Bmax2
Stray Loss
As we all know that transformer functions based on the law mutual induction which states that EMF development in the secondary winding is because of the flux linkage generated by the primary winding. Whereas in practical conditions, the entire flux generated by the primary winding will not have linkage with the complete secondary winding. The amount of flux that does not link with the secondary windings gets wasted and it is the leakage. So, the leakage flux imposes few losses in the transformer and those are called stray losses.
Dielectric Loss
The name of the loss itself indicates that these losses are based on the dielectric ability of the insulating medium used in the device (in general, the insulating medium is oil). Because of this, the transformer’s continuous functionality and the dielectric substance used gets to lose their dielectric ability and generates losses. These losses decrease the transformer’s efficiency, and these can be reduced by continuously testing the insulating substance that is used in the transformer.
Other Types of Losses in a Transformer
Auxiliary Losses – These losses are formed because of the energy used for operating colling pumps or fans which assist in cooling huge transformers.
Magnetostriction Losses – The magnetic flux in the ferromagnetic substance makes the substance physically expand and shrink to so extent for every cycle of the magnetic field and this impact is termed magnetostriction. Because of this impact, a buzzing sound is produced and this leads to magnetostriction losses because of frictional heat.
Mechanical Losses – Along with the magnetostriction, the varying magnetic field produces altering forces in between both the transformer windings. These forces generate vibrations in the close-by metal work along with the buzzing sound and some amount of power gets exhausted.
Additional Losses – Apart from the above-stated losses, the transformer has few additional losses which are because of instability and harmonics. Power losses because of eddy current are dependent on twice the frequency value. So, the existence of harmonic frequencies which are more than the specified frequency level generates additional losses in both the winding and core sections of the transformer.
Transformer Loss Values
While purchasing a transformer, it is more crucial to observe its loss values. The values are termed as ‘A’ and ‘B’. The approach of implementing ‘A’ and ‘B’ factors is mostly used by many electric applications and by huge industrial users in order to take advantage of the future value of load and no-load losses.
The values of ‘A’ shows an approximation for the comparable current price of future no-load losses, whereas the values of ‘B’ show an approximation for the comparable current price of future load losses. Many of the utilities consistently upgrade their averted capacity and energy prices and utilize ‘A’ and ‘B’ values while mentioning the transformer specifications.
These are represented as
TOC = No load losses * A + Load losses * B + C
Where ‘A’ is capitalized price per watt of energy for no-load loss
‘B’ is capitalized price per watt of energy for load loss
‘C’ is the transformer’s primary price along with the sales tax, transportation pricing, and additional service charges
Transformer Efficiency
Similar to other electric devices, the transformer’s efficiency is also stated as
Efficiency = output power/input power
Transformers possess good efficiency levels having an efficiency range between 95 – 98.7%. In order to be high efficiency, ideally, the output and input power values should be equal, and it seems to be not practical to calculate the transformer efficiency through the output/input approach. And the best solution to measure the efficiency is
Efficiency = (input-losses)/ input
= 1 – (losses/input)
In order to attain maximum level of efficiency, consider
Copper loss as Ip2R1
Iron loss as Wi
Then, efficiency 1 – [(Ip2R1+ Wi)/ (V1I1cosФ1)
η = 1 – (IpR1/ V1cosФ1) – (Wi/ V1IpcosФ1)
On applying integration on both sides, we get
dη/dIp = 0 – (R1/ V1cosФ1) + (Wi/ V1Ip2cosФ1)
The efficiency attains maximum value when
dη/dIp = 0, So
(R1/ V1cosФ1) = (Wi/ V1Ip2cosФ1)
(Ip2R1/ V1Ip2cosФ1) = (Wi/ V1Ip2cosФ1)
Ip2R1 = Wi
This defines that transformer efficiency is maximum when copper losses equal to iron losses.
Reduction of various Types of Losses in a Transformer
Even though a transformer comes across various kinds of losses, there are corresponding reduction methods for the removal of various types of losses in a transformer. The losses might not be eliminated completely, but they can be reduced to some extent.
- The foremost thing is to choose an energy-efficient system that possesses a larger core and excellent quality silicon steel for both the copper wires and core section.
- Hysteresis losses can be removed by using extended quality magnetic substances such as silicon steel.
- Eddy current losses are reduced by developing the core sections by piling up very thin sheets.
- Stary losses are eliminated by using thin insulated iron sheets.
- Dielectric losses are eliminated by continuously checking the insulating material.
Know more about Watt’s Law MCQs
On the whole, this article has provided a detailed analysis of various types of losses in a transformer, how they impact the efficiency, and reduction techniques. Know how transformer losses occur because of core magnetization and demagnetization?