What is Transformer Efficiency : Derivation & Affected Factors

We all know that transformer is the most crucial device in many electrical and electronic domains. This is considered as the passive device where the main purpose is to transfer electrical energy from one circuit to another or to many circuits. These are mainly implemented for increasing or decreasing the voltage levels in many applications. As we can state that device performance is noted by its efficiency, similarly transformer performance is known by its efficiency. So, this article mainly focuses on explaining the efficiency of the transformer, its formula, influenced factors, and improvisation methods.

What is the Efficiency of a Transformer?

Transformers are the components where act as a crucial connection between load systems and supply systems. The efficiency of the transformer is influenced by its aging factors and performance. In general, the rating of transformer efficiency lies between 95 – 99%. In the case of high-rated power transformers having minimal losses, the efficiency is nearly 99.6%. During loading circumstances, the input and output calculations are not considered because wattmeter readings certainly undergo few errors. That’s because, while calculating efficiency, it needs SC and OC tests to know transformer losses and core ratings.

The core losses are based on the rated voltage of the transformer whereas copper losses are based on the current flow across primary and secondary windings of the transformer. Thus, the transformer’s efficiency holds more prominence to function it under the scenarios of constant frequency and voltage.

The formula of efficiency of a transformer is given by:

η = {(output power)/(output power + losses)} × 100

Here, the output power is calculated as the product of the fraction of the load and the load’s power factor. And the losses are considered as the sum of (iron loss + loss in the stray load + copper losses in windings + dielectric losses). The iron losses are the sum of eddy current and hysteresis losses where these are shown as follows:

Eddy current loss is Pe = k_ef²Bⁿ_maxt²

Hysteresis loss is Ph = k_hfBⁿ_max

The dielectric loss happens inside the transformer’s oil. For transformers that operate with minimal voltage levels, these losses can be neglected. As the leakage flux is linked to the metallic frame, tank, and other components they develop eddy currents and these are present all across the transformer, so-called a stray loss. These stray losses are based on the load current, so the term stray load loss.

Determination of Transformer Efficiency

For ordinary transformers, the efficiency lies between 96 – 99%. So, it might not be possible to determine with high accuracy by using direct calculation of input and output because the losses are in the range of 1 – 4%. The difference between input and output device readings is so minimal that an error is as little as 0.5% might lead to an error in the range of 15% in the losses.

The best approach for the determination of transformer efficiency is to calculate from SC and OC tests and through this method, the calculation is as follows:

Iron losses are determined as P1 = W0 or P0 measured from the testing of open circuit

Copper losses at the condition of full load are Pc = Wc or Ps measured from testing of short circuit

Copper loss during load with no. of times the full load is I₂² R₀₂ which is x²P_r. Here, I₂ is the secondary current at the condition of full load

So, transformer efficiency is given by

η = (V2I2cosФ)/( V2I2cosФ + Pi + x²P_r)

In the above equation, the impact of the instrument readings is limited to losses so that the entire efficiency from this is very precise when compared with the efficiency level received from the direct loading technique.

Efficiency versus Load

It was noticed that during constant voltage conditions, the transformer’s mutual flux stays constant from no load to entire load where the greatest variation lies in the range of 1 – 3%. So, ion or core losses are observed to be constant irrespective of load. When the kVA output or square of the load, then copper loss varies.

The graph representing variation in a copper loss versus increment in load current is shown below. It also shows efficiency versus load, from the graphical representation it was very clear that the device delivers maximum efficiency even the load is minimal. In practical cases, the efficiency stays constant from 20% to 20% of overload.

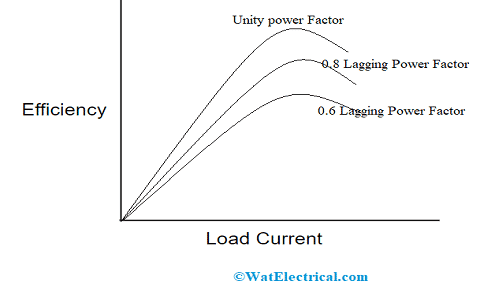
Load Current versus Efficiency of Transformer

At minimal loads, the efficiency is lost due to the reason that constant iron loss but at high loads, the efficiency decreases because of growth in the copper loss. So, it was observed that transformer efficiency level is highest at the point where iron loss and copper loss curves interact.

Transformer’s Maximum Efficiency

The efficiency of transformer considering power factor and load is given by

η = (V2I2cosФ)/( V2I2cosФ + Pi + I₂²R_es)

Here, the value of V₂ is almost constant and the efficiency is based on load current I₂. So, the numerator values become constant, and the transformer achieves high efficiency when the denominator corresponding to I₂ equals zero.

d/dI2 = (V₂I₂cosФ₂ + (Pi/I₂) + I₂R_es) or else

I₂²R_es = Pi which is Iron loss = copper loss

η_max  =  (V₂I₂cosФ₂)/( V₂I₂cosФ₂ + 2Pi) where Pc = Pi

From the above equation, the output current I₂ where the transformer achieves the highest efficiency is

I₂ = sqrt(Pi/R_es)

When ‘X is considered as the fractional part of full load where the transformer’s efficiency is highest, then copper losses equal to x²P_C and iron losses equal to Pi. So, at maximum efficiency condition

x²P_C  = Pi

So, x = sqrt (Pi/Pc)

In terms of KVA, the maximum efficiency is

η_max = sqrt (Pi/Pc) × full load in KVA

This is the maximum efficiency condition of a transformer.

Energy Efficiency

This is also termed as All Day efficiency of the transformer. In a commercial type of transformer, the efficiency is given by

Efficiency = output/input (measured in Watts)

Whereas in few kinds of transformers, it is not possible to find the device performance through efficiency. To explain this, in the distribution type of transformers, they have the primaries energized at every time. Whereas the secondary windings provide minimal load at every time because electricity usage for domestic purposes is mainly at night times.

Due to this, when the transformer’s secondary windings do not provide ant load, then core losses are considered, and copper losses are negligible. The copper losses are measured when loads are present. Thus, copper losses hold more prominence. At these times, the performance is known by comparing the total amount of energy consumption in a day which is given by

All-day efficiency = output/input (both are measured in kWh).

Affected Factors of Efficiency

A few of the factors that affect the efficiency of a transformer are:

• Flux leakage
• Magnetization of the iron core
• The heating effect induced by eddy current
• The heating effect generated in the coil

Methods to Improve Efficiency of Transformer

The approaches of enhancing the transformer efficiency are explained as follows:

1. Insulation – The insulation that exists around the core sheets has to be perfect  so that eddy currents can be eliminated
2. Resistance – The material of primary and secondary windings should be stable which minimizes the electrical resistance
3. Flux Coupling – The transformer windings should be coupled so that flux coupling is maximum.

Thus, this is all about an overview of a transformer & its efficiency, its affected factors, formula, and determination of its maximum efficiency levels. Furthermore, the know-how efficiency of the transformer varies with the power factor?